The Unanimity Rule under a Two-Agent Fixed Sequential Order Voting
Article -
Bannikova, Marina and Giménez-Gómez, José Manuel (2022): "The Unanimity Rule under a Two-Agent Fixed Sequential Order Voting", Games
The voting mechanism is a highly important decision-making procedure used in very different kinds of situations, such as political decisions, jury trials, or the election of the Catholic Pope. It is noteworthy that, in this last situation, the agreement is met only when unanimity arises. This requirement reveals some interesting questions about the voters' behaviour. For instance, in conclaves with misaligned preferences, is it possible to agree on an alternative? If this is the case, which alternative will be implemented? Which voter will have to give up first? When will this occur?
The study of these questions involves a vast number of different contexts, such as the bargaining in legislatures, multilateral bargaining models, and situations with asymmetric information and incomplete information. Recently, it has been studied how agents reach an agreement through a sequential random ordering voting procedure with, potentially, an infinite number of stages. The result of this negotiation process shows that the most patient agent's preferred alternative is chosen in the first round.
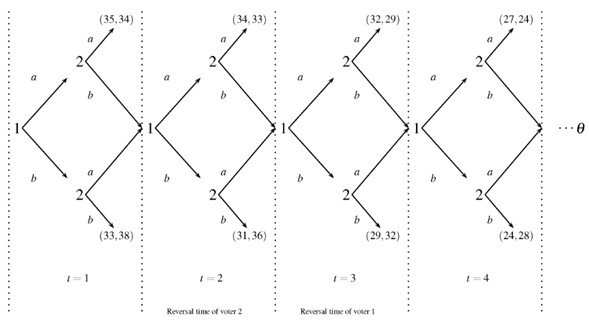
The closest model to the one presented here is a model by Kwiek (2014). He considered a decision-making conclave choosing between two alternatives under a supermajority rule (including unanimity). If a decision is not reached in the first round of voting, then the procedure repeats in the next round, and so on, until the required supermajority is reached. The delay in time is increasingly costly to each player. The question that is asked is: Which rule offers higher utilitarian welfare? In answering this question, he found that there is a subgame perfect Nash equilibrium that leads to a unique voting outcome in the first round. This outcome coincides with the alternative preferred by the pivotal voter with the greater indifference time (or, in other words, impatience degree).
The current approach studies how agents make a unanimous decision over a set of alternatives, assuming potentially an infinite number of voting stages, such that the delay of the decision implies some costs for the voters. Unlike to Kwiek (2014), it is assumed that the ordering of the voters is fixed and the agreement is met by unanimity. Each voter has an impatience degree indicating when it is worth voting for the non-preferred alternative rather than for the preferred alternative. We do not restrict our attention to the cases when voters must be different in their patience. Since both voters know the impatience degree of themselves and the other voter, intuition suggests that the more patient voter will manage to obtain his preferred alternative. We show that the subgame perfect equilibrium is unique: the first voter obtains his/her preferred alternative in the first stage, independently of his/her impatience degree. The result contradicts the one obtained by Kwiek (2014).